Creating Convolutional Neural Network for Handwritten Digit Recognition

In the ever-evolving landscape of artificial intelligence, Convolutional Neural Networks (CNNs) have emerged as a revolutionary force, particularly in the realm of image recognition and computer vision. These sophisticated learning models mimic the human brain’s ability to process visual information, making them incredibly effective for tasks ranging from facial recognition to autonomous driving.

Understanding the basic principles of Convolutional Neural Networks (CNNs) is crucial for several reasons: grasping the basics serves as a stepping stone to more complex concepts in artificial intelligence and deep learning, knowledge of CNN architecture allows to design and tailor neural networks that are optimized for specific tasks, such as image classification or object detection and other benefits.

Basic Concepts

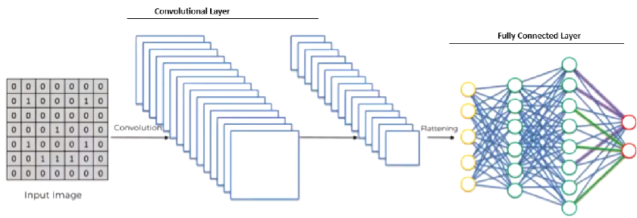
Convolutional Neural Networks (CNNs) are at the forefront of advancements in image recognition and processing. They are engineered to dynamically acquire structural layers of characteristics from visual data. The two pivotal components of CNNs are the Convolutional Layer and the Fully Connected Layer, which work in tandem to process and classify image data and will be described in the details at this article. Before the data can be fed into the Fully Connected Layer, it must be transformed from a 2D feature map into a 1D vector. This process is known as Flattening. Flattening unrolls the feature maps into a single long vector, preparing the data for the next phase of processing. Understanding these three main components is the basis for further study of convolutional neural networks.

Convolutional Layer

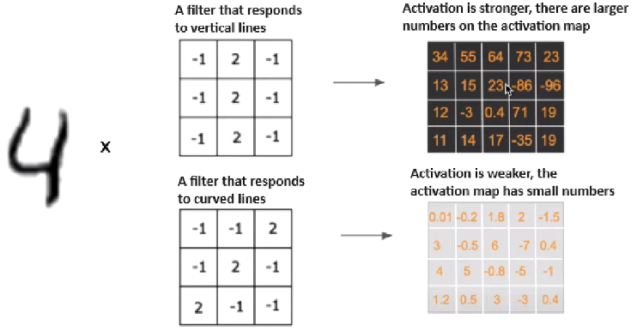
To better understand the principle of operation of the key component of the Convolutional Layer convolutional neural network, let’s ask the question, what distinguishes a four from an eight?

The four has predominantly horizontal and vertical lines, while the eight has diagonal lines.

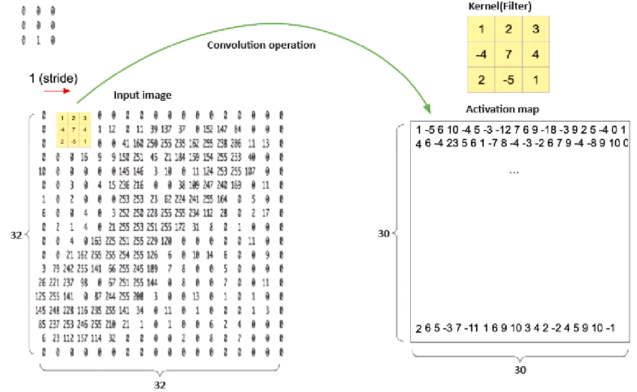
In order to transfer this idea to neural networks, consider the following figure. Any number from 0 to 9 represented in the MNIST dataset is represented as a square matrix of size 32 and the value of each element from 0 to 255.

Next, is needed to introduce the concept of convolution and kernel (filter). The kernel (filter) in neural networks is a matrix of weights that is used in convolutional layers to extract certain features from the input data. The convolution core (filter) is like a light bulb that lights up depending on the required pattern (reacts to lines). The convolution operation in neural networks is a process in which the filter elements are multiplied element by element by the elements of the image on which the filter is located. Activation function (act) – fires after each convolutional layer or fully connected layer to the activation map for each element in the two-dimensional matrix. The stride parameter determines how much the core moves in each iteration. For example, using the kernel to detect vertical and horizontal lines with a four(4) image matrix will result in an activation map with high coefficients.

Looking ahead, the selection of matrix coefficients(weights) is carried out by a library for deep learning, such as Tensorflow, Keras, Pytorch. The mechanism for selecting matrix coefficients (weights) is the same as for Fully Connected Layer and will be discussed further in the corresponding section.

Using multiple Convolutional Layers

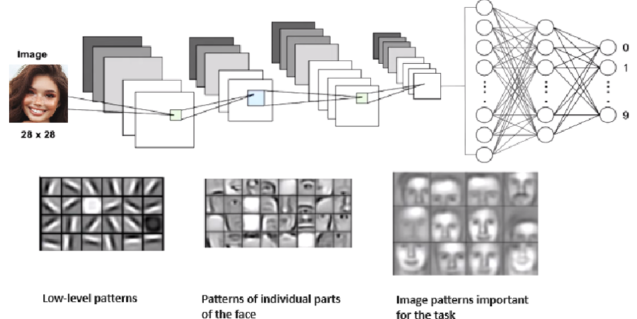
For real-world images, one convolution operation is not enough to extract all the necessary information from the image.

In real life, figures are not only vertical and horizontal lines but contain more complex structures. For example, handwritten numbers, car models, and human faces. For a clearer explanation, we need to consider such a complex structure as the human face. In this case, using a single convolution and a filter that reacts to horizontal lines will not help to understand which person the face belongs to. Therefore, several layers of convolutions are useful. For this task, the convolutional neural network will consist of layers:

1. Low-level patterns
2. Patterns of individual parts of the face
3. Image patterns important for the task

Fully Connected Layer

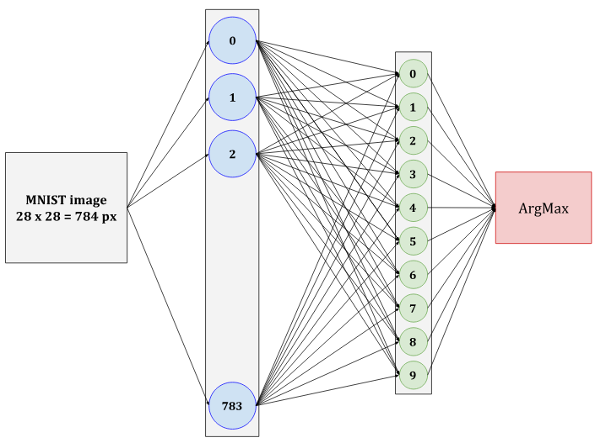
The operating principle of Fully Connected Layer is very similar to the previously discussed Convolutional Layer. A schematic representation of the Fully Connected Layer is shown in the figure.

Confusion between Fully Connected Layers (FC) and Convolutional Layers is common due to different schematic representations. As we can see, the diagram shows neurons instead of quadratic matrices. But the principle of operation is the same as that of the Convolutional Layer discussed above. The first input is an image of size 28 by 28. This means that it has 784 pixels. Each pixel is a separate variable. Each input goes to each of the 128 outputs with its own weight. This turns out to be 100352 weights. The number 128 was chosen at random since it is the one that is optimal in terms of performance and quality for the hidden layer. We will also train 128 free terms (constants) for each of the neurons of the first layer. Overall there are 100480 parameters. For the second layer, the number of outputs is known – 10 digits from 0 to 9. Therefore, 128 x 10 + 10 equals 1290 weights. Next, let’s look at the main differences between Fully Connected Layers (FC) and Convolutional Layers.

Differences between Fully Connected Layer and Convolutional Layer:

1. Functionality:

• Convolutional Layer: Primarily focuses on identifying local patterns within the input data through the use of filters. It is adept at spatial feature extraction and maintains the spatial hierarchy of the input.
• Fully Connected Layer: Aims to integrate the local features identified by the Convolutional Layer to learn global patterns that help in tasks like classification.

2. Connectivity:

• Convolutional Layer: Neurons in this layer are connected only to a local region of the input, preserving the spatial structure.
• Fully Connected Layer: Neurons here are connected to all activations from the previous layer, hence the name ‘fully connected’.

3. Parameter Sharing:

• Convolutional Layer: Employs parameter sharing, meaning the same filter is applied across the entire input, significantly reducing the number of parameters.
• Fully Connected Layer: Does not use parameter sharing; each weight is unique to a specific connection between neurons.

4. Output Representation:

• Convolutional Layer: Produces a 2D activation map that represents various features of the input data.
• Fully Connected Layer: Outputs a 1D vector that represents high-level features derived from the input data after flattening the 2D activation maps.

5. Role in the Network:

• Convolutional Layer: Acts as a feature extractor that identifies important features without being affected by the position within the input.
• Fully Connected Layer: Serves as a classifier that uses the extracted features to make a final prediction or decision.

6. Presence in the Network:

• Convolutional Layer: Specific to CNNs and is not found in other types of neural networks.
• Fully Connected Layer: Common in many types of neural networks, not just CNNs.

Understanding these differences is crucial for designing and implementing effective neural network architectures for various machine learning tasks.

TensorFlow, Keras and MNIST dataset

The most basic form of constructing a neural network to identify handwritten digits ranging from 0 to 9, as discussed in this article – the entry and the exit layers. Since the size of the source image is 28×28 pixels, the size of the input layer is 28×28=784 neurons. Each of the neurons is connected to one of the pixels in the image. The output layer contains 10 neurons, because there are 10 digits from 0 to 9.

MNIST is one of the classic datasets on which it is customary to try all sorts of approaches to classifying (and not only) images. The set contains 60’000 (training part) and 10’000 (test part) black-and-white images of size 28×28 pixels of handwritten numbers from 0 to 9. TensorFlow has a standard script for downloading and deploying this dataset and, accordingly, loading data into tensors, which is very convenient.

Loading the MNIST data set with samples and splitting it by train and test dataset is displayed at the figure:

On the figure are displayed examples of random 20 elements from the MNIST dataset:

Is displayed transformation of values from 255 to 1 in order to follow working with TensorFlow library.

Next, let’s look at creating the convolutional neural network itself. Sequential – serves to describe a neural network model that has an input, hidden and output layer. Flatten converts a multidimensional array into a single-dimensional input. Initially, an input layer with 128 neurons is created. The main convolutional layer contains 128 “neurons”. For activation is used tf.nn.ReLU mathematical function. ReLU is the standard activation function for Convolutional Layers. Range of ReLU is between zero and infinity. This simplifies training and enhances performance.

The output layer matches the 10 recognized digits. This layer helps the network make predictions. In this step is used a softmax activation function: It is like a voting system for the 10 neurons in the second layer. The system converts neuron outputs into probabilities, reflecting the network’s confidence across 10 possible choices. These numbers could be like this: [48.3, 18.3, 4.3, 0.7, 13.2, 1.0, 2.0, 0.1, 1.5, 9.7]. When we use softmax, it makes these numbers more understandable. It condenses the values to ensure their sum equals 1. It’s like saying, “How sure is the network about each option?” After softmax, the numbers turn into this array: [0.483, 0.183, 0.043, 0.007, 0.132, 0.01, 0.02, 0.001, 0.015, 0.097]. Now, these new numbers tell the probabilities. For example, the network is most confident (48.3%) about the first option (0.483).

To build a simple convolutional neural network and recognize handwritten numbers using TensorFlow, you just need to perform four steps:

1. Create an object of the Sequential class, which allows you to create a sequential network model.
2. Flatten the layer to convert the matrix to a single array.
3. Hidden Fully Connected Layer with 128 neurons, in which the main work related to network training will take place.
4. Output Fully Connected Layer with 10 neurons, where each neuron will correspond to a number from 0 to 9.

This sequence of actions is shown in the figure:

Here is displayed the process of compiling and training our neural network:

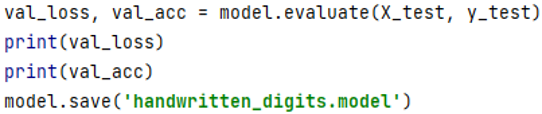
In the next step, we need to evaluate the performance of a deep learning model on a test set of data using Keras. The purpose of this statement is to measure how well the model generalises unseen data and to compare the results with the training and validation sets. A good model should have a low loss and a high accuracy on all sets, and avoid overfitting or underfitting.

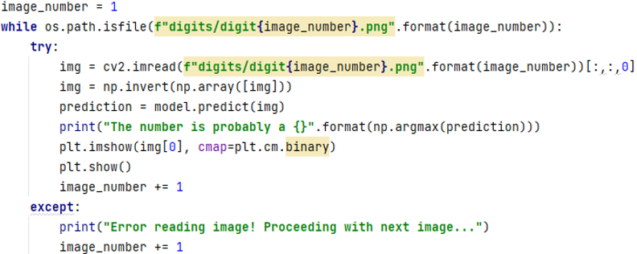
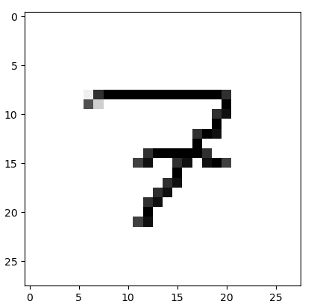
Then we need to recognize handwritten digits from images with the help of the created model. We read the files as an image using cv2 and extract the first channel (assuming it is a grayscale image) using [:,:,0]. It inverts the pixel values of the image using np.invert, so that the background is black and the digit is white. It prints a message saying “The number is probably a {}” where {} is replaced by the index of the highest probability using np.argmax. For example, if the prediction is [0.1, 0.5, 0.2, 0.2, 0, 0, 0, 0, 0, 0], it will print “The number is probably a 5”. Then we display the image using plt.imshow with a binary colormap and plt.show.

The final result with the predicted figures of numbers lying in the recognition folder is shown at the figure. In the current case, the number of recognized files is 5.

Conclusion

In conclusion, the development of a convolutional neural network (CNN) for the recognition of handwritten digits represents an important step in the field of computer vision and machine learning for beginners in this field. This article has demonstrated that through the basic architecture of CNN layers and the application of non-linear transformations, we can achieve good accuracy in classifying individual digits from varied handwriting styles. The understanding of these basic principles paves the way for beginners, how to move on next in the sphere of AI. As we continue to refine the models based on the knowledge described in this article, we are moving closer to creating systems that can not only recognize handwritten digits but also handle more complex structures.

Our experts can help you create software with this feature. Contact us here.